Пам’ятаєте шкільні роки, коли вчитель креслив на дошці загадкові графіки з вертикальними лініями? “Це котангенс”, — казав він, а в очах учнів застигало німе питання. Ми з вами сьогодні розберемося з цією функцією так, щоб вона стала зрозумілою і корисною.
Що таке котангенс?
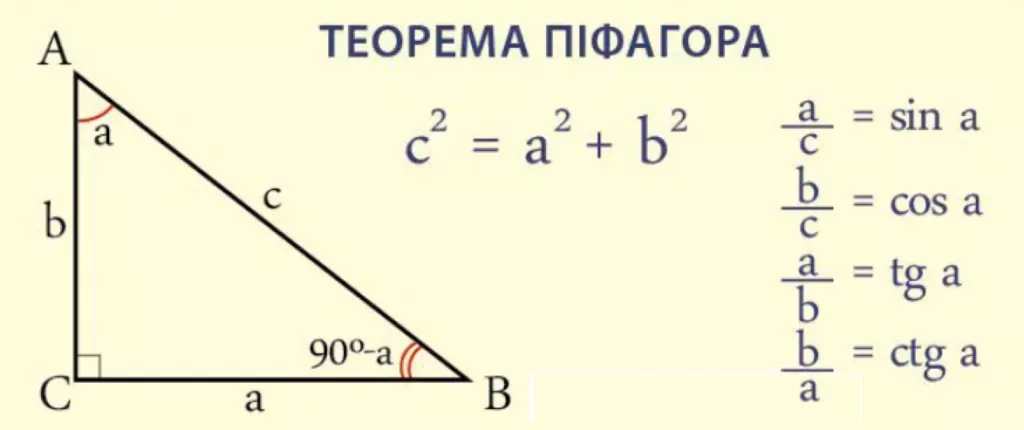
Котангенс — це тригонометрична функція, яка показує відношення прилеглого катета до протилежного в прямокутному трикутнику. Записуємо її як ctg α або cot α.
У математичній формі:
ctg α = прилеглий катет / протилежний катет
Або через інші тригонометричні функції:
ctg α = cos α / sin α = 1 / tg α
Коли ви стоїте на березі та дивитесь на маяк, кут між горизонтом і напрямком на вершину маяка можна виразити через котангенс. Він покаже відношення відстані до маяка відносно його висоти.
Геометрична картина котангенса
На одиничному колі котангенс кута — це відстань від початку координат до точки перетину дотичної з віссю Oy.
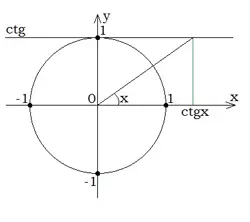Уявіть, що ви стоїте в центрі кола радіусом 1 метр. Проведіть промінь під кутом до горизонту. Тепер уявіть вертикальну лінію, яка торкається кола. Відстань від центру до точки перетину променя з цією вертикальною лінією — це і є котангенс вашого кута.
Спробуйте побудувати це на папері, і ви побачите, як оживає суха формула.
Властивості котангенса
Котангенс має такі ключові властивості:
- Область визначення: всі числа, крім π·n, де n — ціле число (функція не існує, коли sin α = 0)
- Область значень: всі дійсні числа
- Функція непарна: ctg(-α) = -ctg(α)
- Періодичність: період дорівнює π (ctg(α + π) = ctg(α))
Коли синус наближається до нуля, котангенс зростає до нескінченності. Це створює вертикальні лінії на графіку — асимптоти.
Ви можете спостерігати подібний ефект, коли світло проходить через щілину — при певних кутах інтенсивність світла різко зростає, майже як асимптота котангенса.
Зв’язок з іншими функціями
Котангенс тісно пов’язаний з іншими тригонометричними функціями:
- ctg α = cos α / sin α
- ctg α = 1 / tg α
- ctg²α + 1 = 1 / sin²α
Це як у родині — всі функції пов’язані між собою. Знаючи одну, ви можете знайти інші.
У шкільному трикутнику ці зв’язки дозволяють нам розв’язувати задачі різними способами. Якщо ви знаєте синус і косинус, ви вже знаєте котангенс.
Графік котангенса
Графік котангенса — це крива, яка перетинає вісь Ox у точках π·n + π/2. Він має вертикальні асимптоти в точках x = π·n.
Уявіть американські гірки, які нескінченно підіймаються вгору, потім різко падають униз, проходять через нуль і знову підіймаються. Це схоже на графік котангенса.
Коли ви креслите графік, звертайте увагу на ключові точки:
- x = π/4: ctg(π/4) = 1
- x = 3π/4: ctg(3π/4) = -1
Застосування котангенса
Котангенс застосовують у багатьох сферах:
- У фізиці — для розрахунку коливань і хвиль
- В інженерії — для обчислення нахилів і кутів
- У навігації — для визначення відстаней і напрямків
Коли будівельник вимірює нахил даху або моряк визначає курс корабля, вони часто використовують котангенс, навіть не згадуючи цю назву.
Приклад розв’язання задачі
Задача: Знайти висоту дерева, якщо відстань від спостерігача до дерева 15 м, а кут між горизонтом і напрямком на верхівку дерева 30°.
Розв’язання:
- Позначимо висоту дерева як h
- За означенням: ctg 30° = 15 / h
- ctg 30° = √3
- Тому: √3 = 15 / h
- h = 15 / √3 ≈ 8,66 м
Цей приклад показує, як котангенс допомагає вирішувати практичні задачі.
Котангенс — не просто абстрактна функція. Це інструмент, який допомагає нам описувати світ навколо. Від шкільної математики до інженерних розрахунків — ця функція працює для нас.
Наступного разу, коли побачите вертикальну лінію на графіку, посміхніться — ви вже знаєте, що це котангенс нагадує про себе. Спробуйте знайти котангенс у повсякденному житті, і математика стане ближчою та зрозумілішою.
Пишу про все, що надихає та змушує задуматися. Маю журналістську освіту та багато років досвіду у створенні пізнавальних матеріалів. Захоплююсь наукою, культурою та історіями успіху. Шукаю цікаве в усьому, аби ділитися знаннями, які допомагають відкривати нові горизонти, бачити красу світу та отримувати корисні поради для життя.
