Як додати дроби з різними знаменниками: просте пояснення для кожного
Чи коли-небудь ви стикалися з проблемою, коли потрібно додавати дроби, а знаменники різні? Здається, що це складно, але насправді, як тільки зрозумієш основи, усе стає набагато простіше. У цій статті я поясню, як додавати дроби з різними знаменниками так, щоб ви могли без зусиль розв’язувати подібні задачі на будь-якому рівні.
Що таке дроби з різними знаменниками?
Дроби з різними знаменниками — це дроби, у яких нижні числа (знаменники) відрізняються. Наприклад, 1/4 і 2/5 — це два дроби з різними знаменниками. Якщо б знаменники були однаковими, ми могли б їх просто додавати чи віднімати, але в такому випадку треба знайти спільний знаменник, що дозволить звести дроби до однакового знаменника.
Важливо розуміти, що робити це правильно необхідно, щоб не заплутатися у розрахунках. В іншому разі результат може бути неправильною відповіддю.
Алгоритм додавання дробів з різними знаменниками
Для того щоб додати дроби з різними знаменниками, потрібно виконати кілька простих кроків. Розглянемо це на прикладі:
Крок 1: Знайти найменший спільний знаменник (НСК)
Щоб дроби можна було додати, треба, щоб їх знаменники були однаковими. Для цього шукаємо найменший спільний знаменник (НСК). Найлегше це робити за допомогою множників знаменників кожного дробу. Наприклад, для дробів 1/4 і 1/6 треба знайти найменший спільний знаменник для 4 і 6. Це буде 12.
Крок 2: Перевести дроби до спільного знаменника
Коли НСК знайдено, треба перевести кожен дріб до цього знаменника. Для цього множимо чисельник і знаменник кожного дробу на таке число, яке дасть знаменнику потрібний НСК.
Наприклад, щоб перевести 1/4 в дріб з знаменником 12, треба помножити чисельник і знаменник на 3 (бо 4 * 3 = 12). Тобто, 1/4 стає 3/12.
Щоб перевести 1/6 в дріб з знаменником 12, множимо чисельник і знаменник на 2 (бо 6 * 2 = 12). Тобто, 1/6 стає 2/12.
 Крок 3: Додати чисельники
Крок 3: Додати чисельники
Тепер, коли знаменники рівні, ми можемо просто додати чисельники дробів. У нашому прикладі:
3/12 + 2/12 = 5/12.
Ось і все! Це такий простий алгоритм для додавання дробів з різними знаменниками.
Крок 4: Спрощення дробу
Якщо після додавання дробів результат можна спростити (наприклад, поділити чисельник і знаменник на спільний дільник), обов’язково це зробіть.
У нашому прикладі 5/12 вже не можна спростити, оскільки 5 і 12 не мають спільних дільників.
Приклад додавання дробів з різними знаменниками
Давайте розглянемо ще один приклад, щоб краще зрозуміти процес.
Нам потрібно додати дроби 3/8 і 5/12.
Знайдемо НСК для 8 і 12. Це буде 24.
Тепер переведемо дроби до спільного знаменника:
3/8 множимо на 3 (бо 8 * 3 = 24), отримаємо 9/24.
5/12 множимо на 2 (бо 12 * 2 = 24), отримаємо 10/24.
Додаємо чисельники: 9/24 + 10/24 = 19/24.
І результат — 19/24, який вже не можна спростити.
Поширені помилки при додаванні дробів з різними знаменниками
Хоча алгоритм здається простим, часто можна зустріти деякі поширені помилки, які варто уникати:
Невірне знаходження НСК: Це одна з найбільш поширених помилок. Якщо ви неправильно знайдете НСК, то всі наступні кроки будуть помилковими.
Невірне переведення дробів до спільного знаменника: Це також часта помилка, коли учень або студент не помножує правильно чисельники і знаменники.
Невірне додавання чисельників: Потрібно обов’язково додавати тільки чисельники, а знаменники залишаються незмінними після приведення дробів до спільного знаменника.
Не спрощення результату: Якщо дроби можна спростити, обов’язково це робіть, щоб результат був у найпростішій формі.
Пам’ятайте: для досягнення правильного результату важливо дотримуватися всіх етапів, а також бути уважними до кожної деталі.
 Практичні вправи
Практичні вправи
Для того, щоб закріпити навички додавання дробів з різними знаменниками, спробуйте розв’язати кілька вправ:
Додати дроби 3/5 і 2/7.
Додати дроби 4/9 і 5/6.
Додати дроби 2/3 і 4/15.
Спробуйте виконати ці вправи самостійно, і ви побачите, як швидко освоїте техніку додавання дробів!
Додавання дробів з різними знаменниками може здаватися складним, але це лише на перший погляд. Як тільки ви зрозумієте, як працює алгоритм, зможете легко додавати дроби будь-якої складності. Просто пам’ятайте, що найголовніше — це правильно знаходити найменший спільний знаменник і переводити дроби до однакового знаменника. Вправа зробить вас майстром у цій справі.
Тепер, коли ви знаєте основи, не бійтеся додавати дроби з різними знаменниками. Приділяйте цьому трохи часу, і ви будете вражати своїх друзів і вчителів своєю математичною майстерністю!

 Крок 3: Додати чисельники
Крок 3: Додати чисельники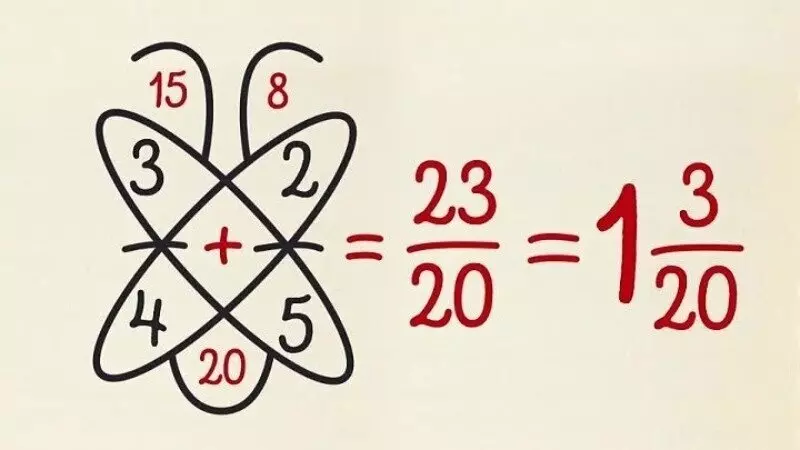 Практичні вправи
Практичні вправи